Where the techniques of Maths
are explained in simple terms.
Probability - Probability trees.
Test Yourself 2 - Solutions.
- Algebra & Number
- Calculus
- Financial Maths
- Functions & Quadratics
- Geometry
- Measurement
- Networks & Graphs
- Probability & Statistics
- Trigonometry
- Maths & beyond
- Index
| Basic | 1. 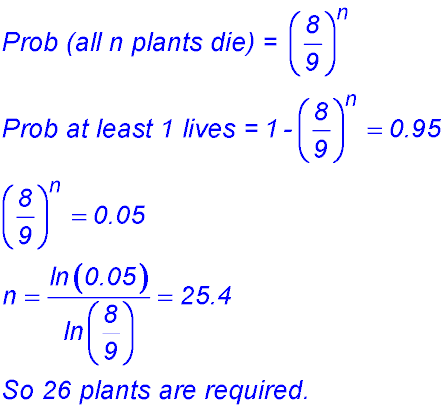
|
2. Answer.Pr(no 6) = 0.162 (3 dp). |
|
3. Answer.(i) (a) Pr(GG) = 0.36 (ii) Pr(GB) = 0.48. (iii) Pr (BB) = 0.16. |
|
| 4. | |
| 5. | |
6.
Answer.(i) Pr (passes one) = 0.188 (ii) Pr (passes all 3) = 0.336 (iii) Pr (at least 1) = 0.976. |
|
7. Answer.(i) Pr(correct) = 1/10,000 (ii) 1 - (1/10)4 = 3,439/10,000 (iii) 1/1,000 (iv) 1/24 |
|
8. 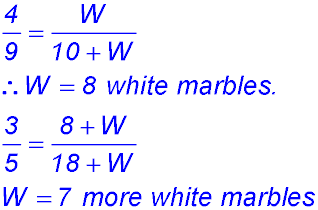 |
|
| 9. | |
| Constant probability. | 10. (i) What is the probability that David wins on his first turn? Prob = 1/5. (ii) determine the probability that David eventually wins the game. On 1st throw, David wins with a probability 1/6. To win on his 2nd throw, David must lose on his first throw and Jack must lose on his first throw and then David must win. So (5/6)2 × 1/6. To win on his 3rd throw, David has to lose both his first 2 throws and Jack must lose both of his first 2 throws and then David must win on his third throw. So (5/6)4 × 1/6. So we have a series: 1/6 + (5/6)2 × 1/6 + (5/6)4 × 1/6 + ... Sum to infinity = 6/11.
|
| With replacement | |
| 16.
|
|
| 17. | |
| 18. | |
| 10. | |
| Without replacement | 11.(i) 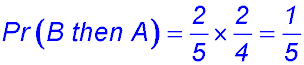 . .
(ii) |
| Harder | 26. (i) Prob (not seeing a whale) = 0.6 (which is the complement).
Prob (not seeing any whales in 5 days) = 0.62 = 0.077. (ii) Prob (seeing at least 1 whale in n days) has to > 0.9. ∴ Prob (≥ 1 whale) = 0.9 > 1 - 0.6n 0.6n > 0.1 n= log0.60.1 - so n > 4.5 - hence 5 days. |
| Incomplete trees. | |
.
.
.
